Kelly Formula / 凱利公式 － 風險控管

投資 vs 投機 vs 賭博, 不管你自認為是使用以上三種策略的那一種人, 今天要介紹的是一門讓你在這條路上可以走得更遠、更久的準則－Kelly Formula, 先來上一堂數學課吧!

Kelly Formula

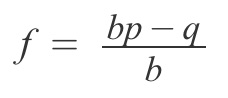
• b : 賠率 (獲勝後的報償比上本金的比例, ex. 賭上 1 元, 獲勝可拿回 1+b 元)
• p : 勝率 (獲勝的機率)
• q : 敗率 (1-p)
• f : 為使用現有資金應進行投注的比例

Kelly Formula 為求最大期望值時, 應投入的資金比例 (其中 b、p、q 皆為不變常數)
from Wiki

證明

Definition

• X_n : 表示 經過 n 次賭局後所剩的資金 (n=0, 表示初始資金)
• W_n : 表示 經過 n 次賭局, Win 的次數
• L_n : 表示 經過 n 次賭局, Loss 的次數

Two Cases

• X_n = X_n-1 ( 1 + bf ) Win case, 剩餘金額 = 前次金額 * (1 + 賠率*前次投注的比例)
• X_n = X_n-1 ( 1 - f ) Loss case, 剩餘金額 = 前次金額 * (1 - 前次損失的比例)

更進一步可以理解

X_n = X₀ ( 1 - f ) ^Ln ( 1 + bf ) ^Wn ... (式1)
剩餘金額 = 初始金額 * (失敗 case)^失敗次數 * (勝利 case)^勝利次數

參考文獻中更進一步的將 Loss Case 中的賠率 (賠給對方), 另外定義為 a, 所以整理得到的公式會如下

X_n = X₀ ( 1 - af ) ^Ln ( 1 + bf ) ^Wn ... (式2)

而 (式1) 只是當 a=1 的 special case (表示當輸了時, 會造成該次投注金額全部損失)

Reference Betting with the Kelly Criterion, Jane Hung (June 2,2010)

這邊先以 (式2) 來求 f 的最佳值, 首先對 方程式 的左右兩側同時

1. 除以 X₀
2. 取 ln (ln = log_e)
   因為 ln 為嚴格遞增函數, 所以對 方程式 兩側作用後, 不影響求極大值的條件。 (若 x₁、x₂ 為實數 且 x₁>x₂, 則 f(x₁) > f(x₂)恆成立, 滿足此條件的 f(x) 稱為 嚴格遞增函數)
3. 除以 n (當 n>0 時, 也可視為嚴格遞增)

透過使用下列對數律

• log_a X*Y = log_a X + log_a Y
• b * log_a X = log_a X ^b

化簡後如下 ... (式3)

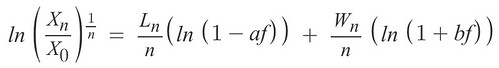
新定義一個函式為 G(f) = (式3), 因 L_n / n = q、W_n / n = p (來自於 p、q 本身的定義為勝率跟敗率), 所以得到

G(f) = q (ln (1-af)) + p (ln (1+bf))

目前問題已經轉化為要求 G(f) 的最大值時, f 應該使用多少?

這邊一階微分在數學上的意義是斜率, 所以當我們今天要找極大值相當於我們要找出斜率 = 0 的點, 所以我們先找出 G'(f) = 0 的 f 值有哪些?

使用 Chain Rule 技巧可以得到下面結果

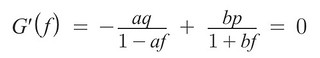
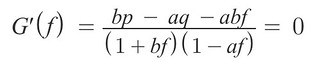
因為分母 =\= 0, 所以這邊僅需要求分子 bp - aq- abf = 0 的 f 解, 透過移項後即可得到 G(f) 的極值出現在 f 為何時 (當然這邊其實還要用二階微分來求函數的凹性, 確認求出的 f 值代入 G(f) 是極大還是極小值, 但這邊省略請直接參考 Jane 的文獻)

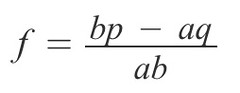
得到 (式2) 的解後, 就可以知道 (式1) 得到的 Kelly Fromula 僅是當 a 為 1 時的特殊解。

推薦Online好用的數學工具

The Stock Market

股票市場上的賭局並非使用固定的賠率看待, 所以這邊引入了隨機變數的概念, 用 X 表示每單位可拿回的金額 (相當於之前 Kelly Formula 裡的賠率 b), P(X = s) 則表示當 X 為 s 時發生的機率。

隨機變數參考網站

又因為今天在設法求出最佳投注資金比例 f 時, 重點不在於整個市場的機率分佈呈現是如何, 所以對機率分佈上做了以下的假設

P(X = μ + σ) = P(X = μ − σ) = 0.5 ... (式4)

• μ 為平均值
• σ 為標準差

而在資金 Y 變化的公式則是由下式表示

Y_n = Y_n-1 (1 + (1-f)r + fX), (r 表示 未 進行投注的資金獲得的報償比例)

解讀為

現有剩餘資金 = 前次剩餘資金*(1 + 未投注市場比例*未投注報償比 + 投注市場比例*投注市場報償比) 

當今天進行了 n 次的投注後, 嘗試列出 現有資金 與 初始資金 間的關係, 所以這邊重新做了一次以下的假設, 使得我們經過 n 次投注後得到的總 μ, σ² and r 仍相同 (意味要將 μ, σ² and r 平均分散在 n 次的投注中)

• 標準差 σ' 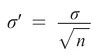(因為要令 σ'² * n = σ²)

• 回報率 μ' 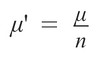(因為要令 μ'* n = μ)

• 其他投資回報率 r' 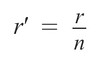(因為要令 r'* n = r)

• 將以上的變量代入一開始假設的機率分佈

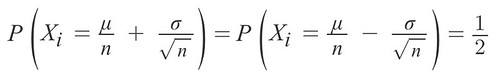
可以導出 Y_n 與 Y₀ 的關係式

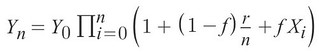
將 Y₀ 移項至左式, 再兩邊同取 ln 後

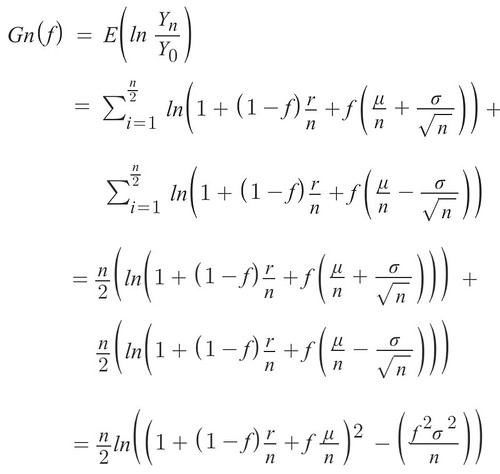
回到 Kelly Formula 的討論, 我們仍是要求 G_n(f) 的極大值出現在 f (資金下注比例) 為何時?

在這部分的推導上是先將 G_n(f) 以 Maclaurin 級數展開, 並令 n->∞ 時對多項式來求極值。

(詳細的步驟可以參考我的計算過程, 跟 Jane 的有些微出入, 我猜她可能沒有實際推導後面的展開式, 所以才會在微分的結果上寫錯)

最後我們總算可以導出適用於市場的 Kelly Criterion。